Editions Petite Elisabeth. Des ressources pédagogiques en mathématiques, physique et chimie pour les collèges, les lycées et la formation professionnelle (CAP, BEP, BP et bac pro).

Résumés de cours

Calculs en ligne

Graphiques en ligne

Ressources

Graphiques en ligne
Étudier les variations d'une fonction et tracer sa courbe représentative

Pour étudier les variations de la fonction f, vous calculez sa dérivée f ' et étudiez le signe de f '(x).

Vous pouvez choisir un point A de la courbe de f et visualiser la tangente à la courbe au point A d'abscisse x_A.
La tangente en A est une droite de coefficient directeur f '(x_A).

• Si f '(x_A) < 0 alors la tangente en A est dirigée vers le bas : la fonction f est décroissante.
• Si f '(x_A) = 0 avec un changement de signe de f '(x) avant et après x_A alors la tangente en A est horizontale (parallèle à l'axe des abscisses) et la fonction f admet un extremum local (minimum ou maximum) en A.
• Si f '(x_A) > 0 alors la tangente en A est dirigée vers le haut : la fonction f est croissante.

Afficher/Masquer les règles d'utilisation et un exemple d'options d'affichage

Intervalles (x) et (y) Taper des entiers relatifs. Graduations (x) et (y) Graduation (x) →↑ Toutes les unité(s) Graduation (y) Toutes les unité(s) Quadrillages Vertical Toutes les unité(s) Horizontal Toutes les unité(s) Vertical (+) Div : 2 5 10 Horizontal (+) Div : 2 5 10 Vertical (++) Div : 2 5 10 Horizontal (++) Div : 2 5 10 Dimensions du graphique Largeur maxi : 700 pixels Largeur (pixels) Hauteur (pixels)

# Fonctions usuelles f(x) = x2 → Fonction carrée f(x) = x3 → Fonction cubique f(x) = 1/x (x ≠ 0) → Fonction inverse f(x) = ln x (x > 0) → Fonction logarithme népérien f(x) = ex → Fonction exponentielle f(x) = cos x → Fonction cosinus f(x) = sin x → Fonction sinus # Fonctions paramétrables f(x) = ax2 + bx + c a = b = c = avec a ≠ 0 f(x) = ax3 + bx2 + cx + d a = b = c = d = avec a ≠ 0 f(x) = a/x + bx + c (x ≠ 0) a = b = c = avec a ≠ 0 Visualiser la tangente à la courbe de f au point A d'abscisse

Exemple : étudier les variations de la fonction f.

La fonction f est définie par f(x) = -2x³ + 3x² + 4x + 5.

Données :

a = -2 ; b = 3 ; c = 4 et d = 5.

On calcule sa dérivée f ' et on étudie son signe. f ' est définie par f '(x) = -6x² + 6x + 4.

Interprétation graphique de la dérivée :

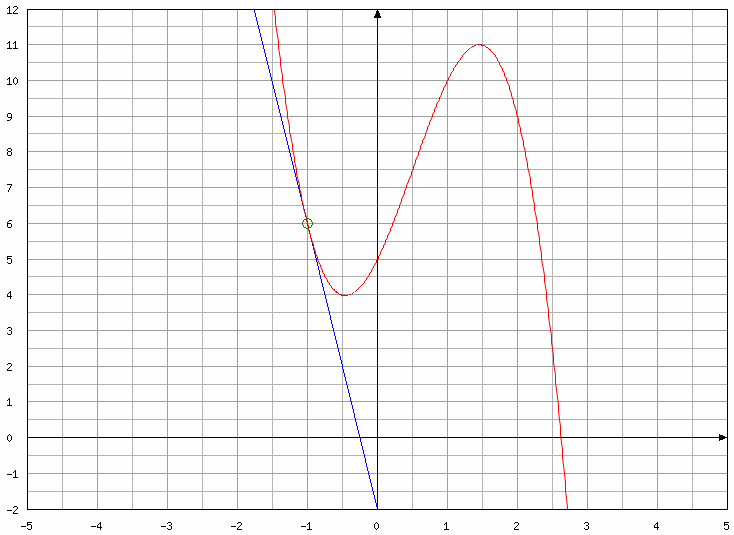
Soit A (x_A ; y_A) un point de la courbe représentative de f.

La tangente à la courbe au point A est une droite de coefficient directeur f '(x_A).

Si x_A = -1 alors f '(x_A) = f '(-1) = -8 < 0.

La tangente en A est dirigée vers le bas : la fonction f est décroissante.

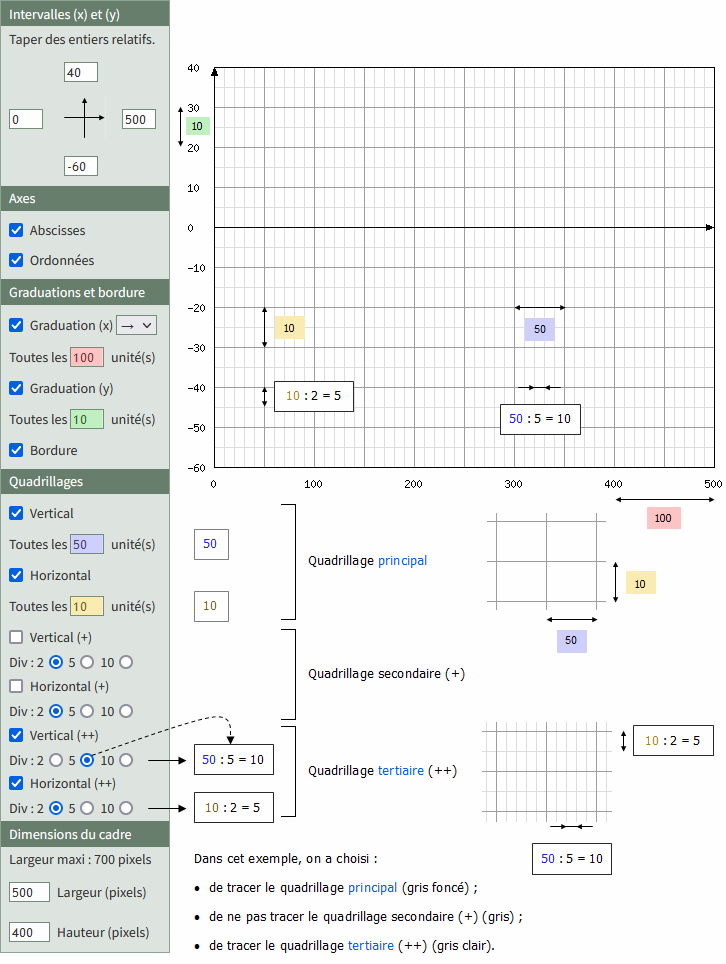
Options d'affichage choisies :

1. Intervalle (x) : [-5 ; 5] (uniquement des entiers relatifs).
2. Intervalle (y) : [-2 ; 12] (uniquement des entiers relatifs).
3. Les graduations (x) et (y) sont tracées toutes les 1 unité à partir de 0 (origine).
4. L'option → est sélectionnée : la graduation (x) située en bas du graphique est horizontale.
5. Les quadrillages vertical et horizontal principaux (couleur gris foncé) sont tracés toutes les 1 unité à partir de 0 (origine).
6. Les quadrillages secondaires (+) (couleur gris) sont tracés en divisant les quadrillages principaux par 2.
7. Dimensions du graphique : 700 pixels (largeur) sur 500 pixels (hauteur).